

My main area of research is strong-field and attosecond physics (theory). However, I have also been
active in other areas such as mathematical physics (non-Hermitian Hamiltonian systems) and short-
pulse propagation in nonlinear media. My work in this field encompasses high-order harmonic
generation (HHG) and attosecond pulses, above threshold ionization (ATI), stabilization and
nonsequential double and multiple ionization (NSDI, NSMI). I also seek novel approaches for matter in
strong laser fields, in an interdisciplinary effort linking strong-field physics, mathematical physics and
quantum chemistry.
Research Lines
Our main area of research is strong-field and attosecond physics (theory). Our work in this field encompasses high-order harmonic generation (HHG) and attosecond pulses, above threshold ionization (ATI), stabilization and nonsequential double and multiple ionization (NSDI, NSMI). We also seek novel approaches for matter in strong laser fields, in an interdisciplinary effort linking strong-field physics, mathematical physics and quantum chemistry. These lines of research have evolved from a unified research vision, very often overlap, and strong-field phenomena may be used for imaging and control of electron dynamics. This control can be exerted by using tailored fields in, for instance, appropriately chosen targets. Work beyond attoscience includes areas such as mathematical physics (non-Hermitian Hamiltonian systems) and short-pulse propagation in nonlinear media.


Novel Strong-Field Approaches
We bring approaches & tools from other areas to strong-field physics, and also develop our own. Examples are Initial Value Representations, Bohmian trajectories, Wigner quasi-probability distributions & the Coulomb-Quantum Orbit Strong-Field Approximation (CQSFA) developed at UCL. The latter is at the forefront of Coulomb-distorted strong-field approaches.
Family tree of orbit-based approaches employed in strong-field and attosecond science. From C. Figueira de Morisson Faria and A.S. Maxwell, Rep. Prog. Phys. 83, 034401 (2020).
Electron-electron correlation
We have applied semi-analytic methods to electron-electron correlation in intense fields, whose archetypical manifestation is laser-induced nonsequential double ionization (NSDI). Our recent work has focused on the recollision-excitation with subsequent ionization (RESI) pathway in NSDI. We demonstrate that it can potentially be used for attosecond imaging and that quantum-interference effects may survive focal averaging and integration over degrees of freedom. This calls into question the long-held assumption that NSDI is classical.

Quantum-interference fringes in correlated electron-momentum distributions for pulses of different lengths. From A.S. Maxwell and C. Figueira de Morisson Faria, Phys. Rev. Lett. 116, 143001 (2016).

Photoelectron momentum distribution calculated with the Coulomb-Quantum Orbit Strong-Field approximation revealing a wide range of holographic structures that are unavailable via more standard semi-analytic methods.
Strong-field ionization & Photoelectron holography
Our studies in strong-field ionization encompass many subareas, such as tunneling dynamics in phase space, above-threshold ionization, and, in recent years, ultrafast photoelectron holography. Earlier studies deals with the importance of pulse shapes in stabilization.
Photoelectron holography brings together high currents and ultrafast time resolution, and uses phase differences between qualitatively distinct quantum electron pathways to reconstruct a target. Because the residual potentials influence the electron propagation in the continuum, it is a great testing ground for novel Coulomb distorted methods, such as the CQSFA. We have performed one of most comprehensive studies of quantum interference in this context.
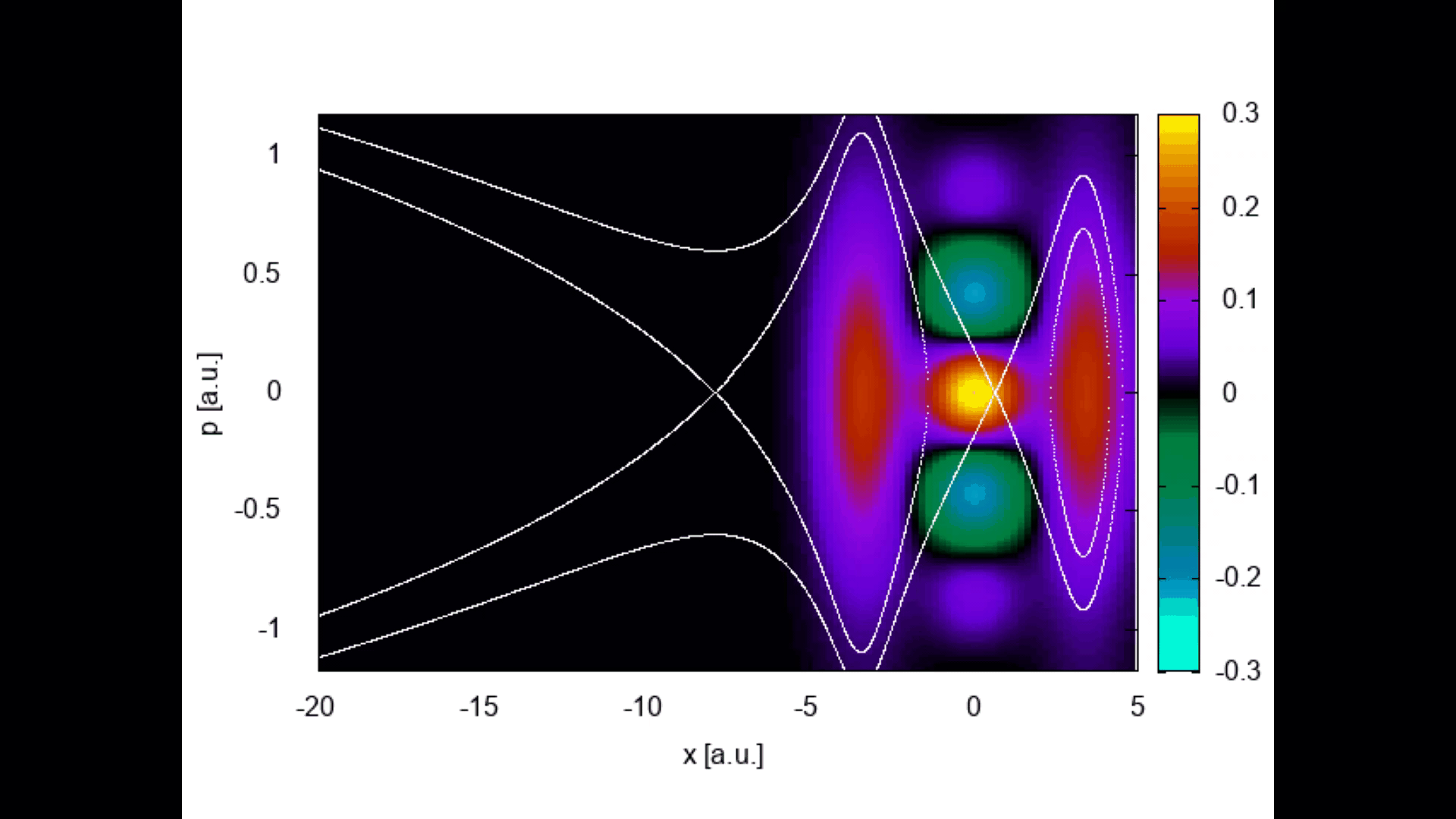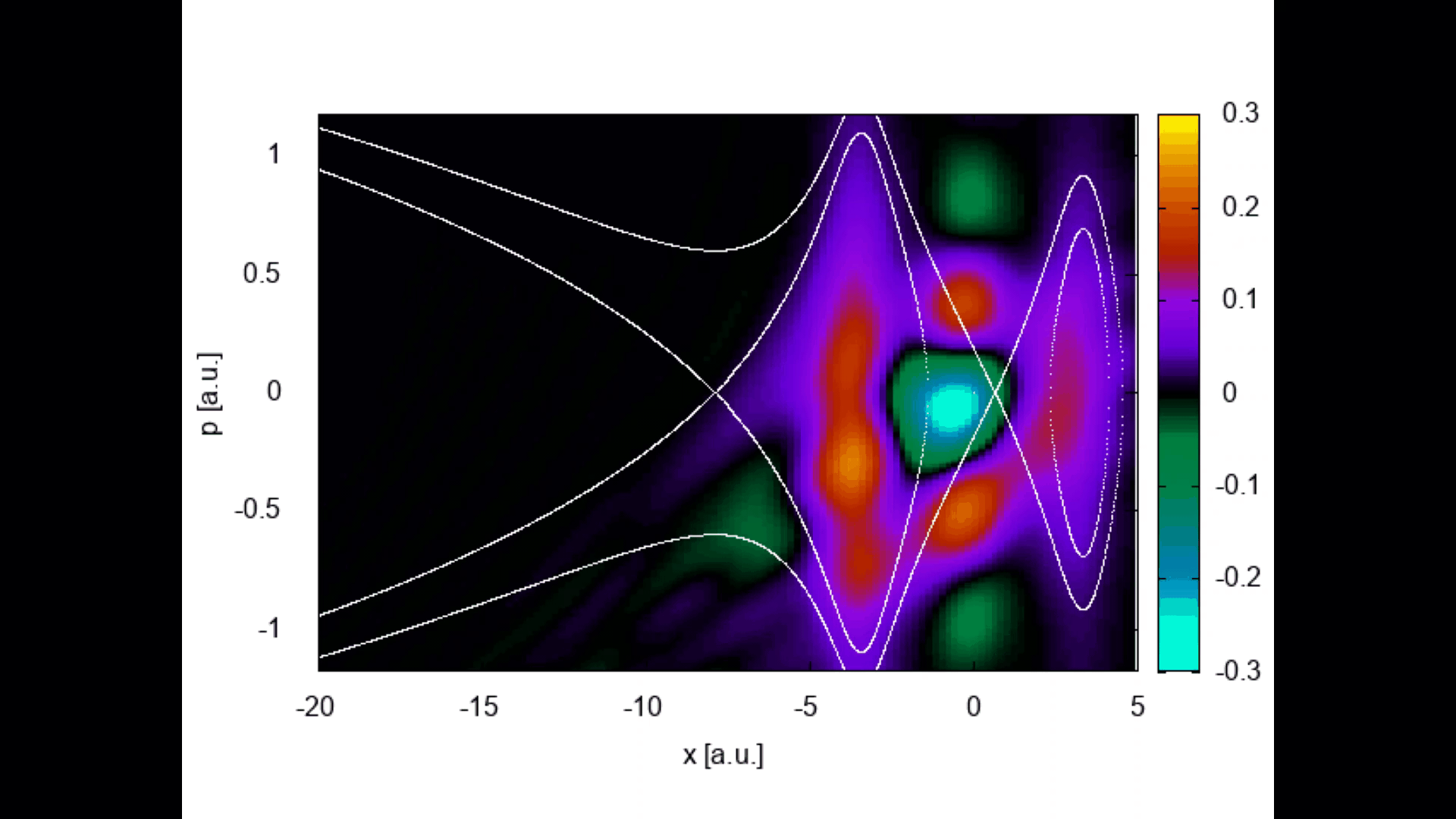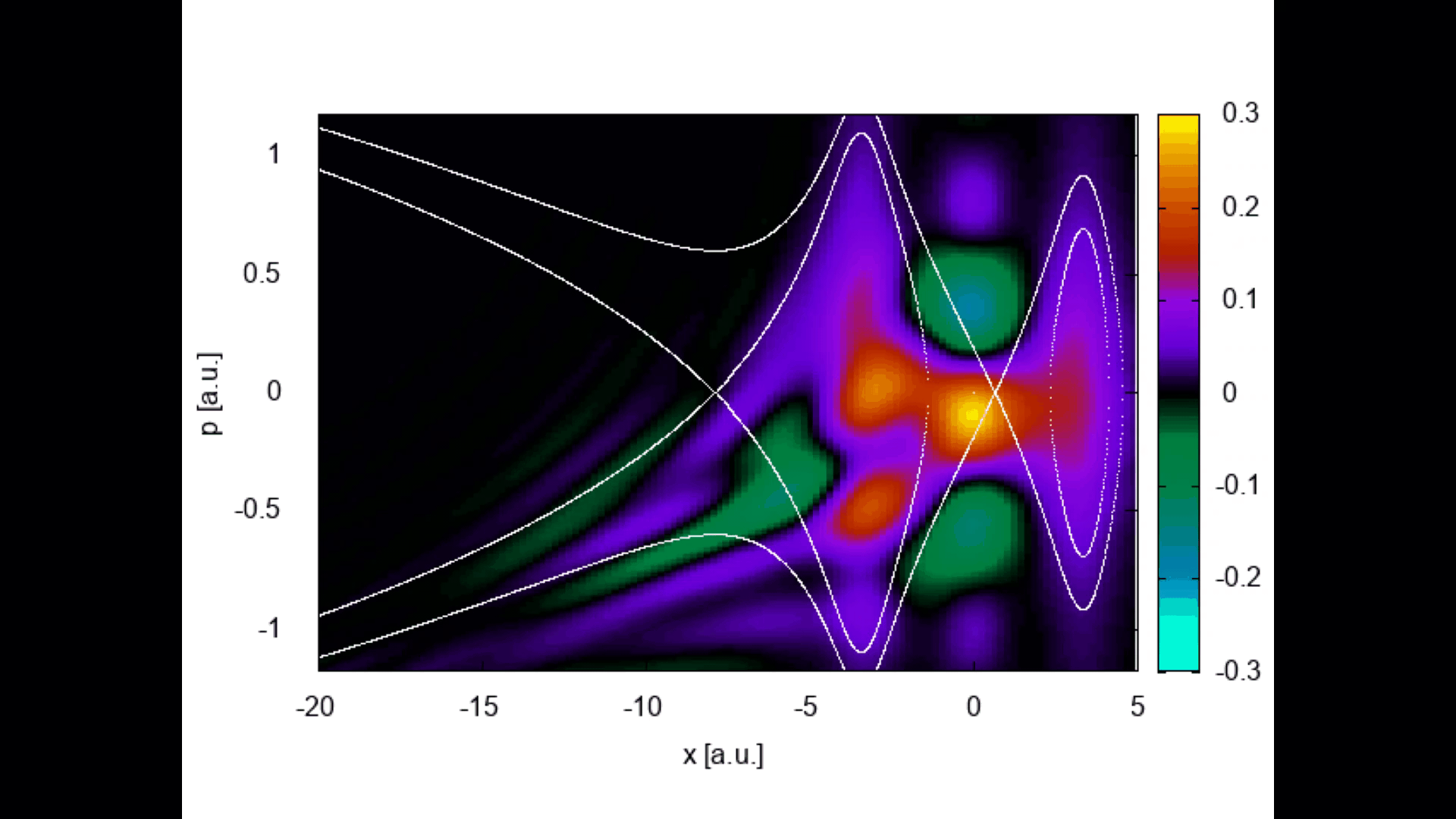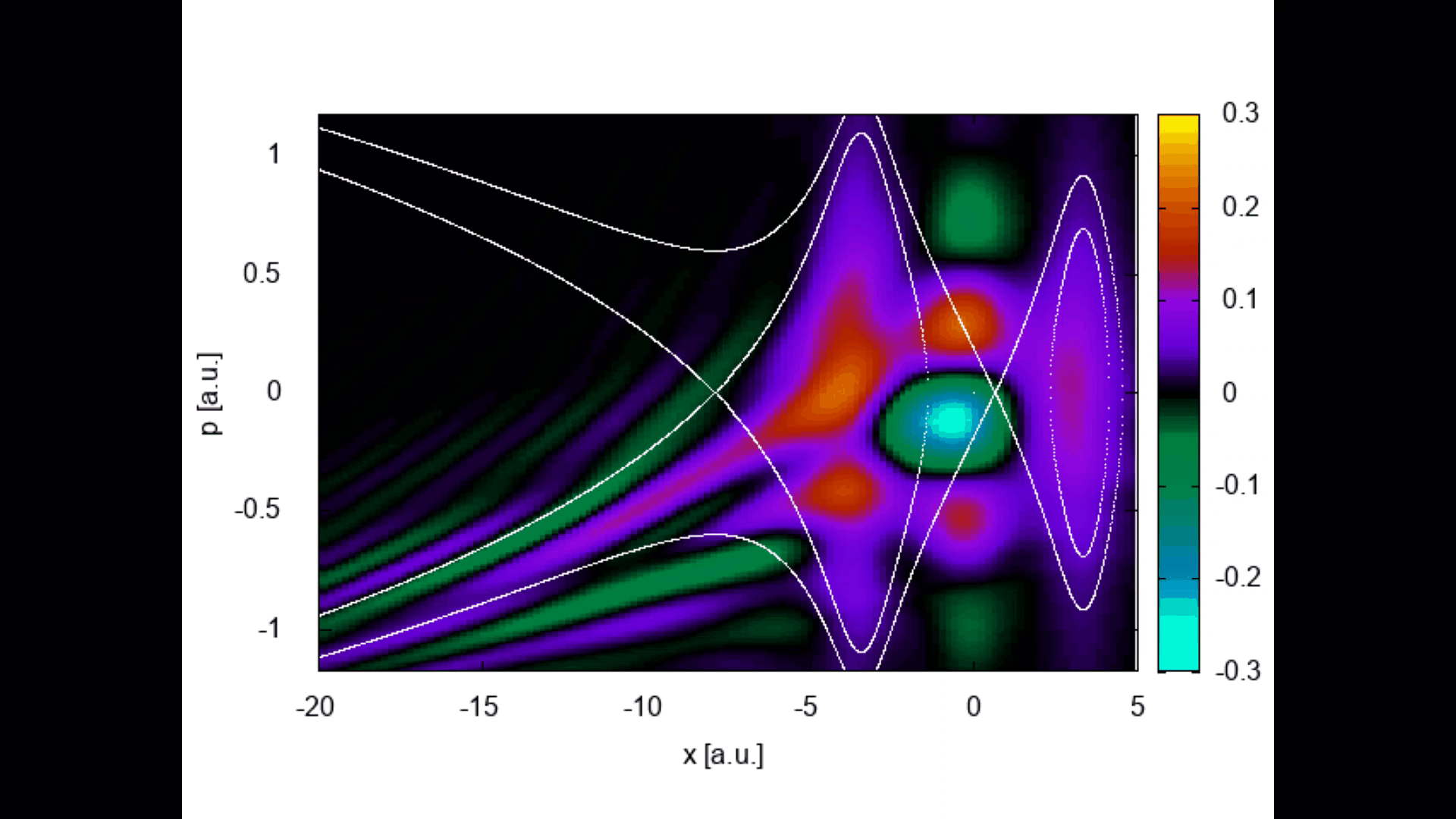
Tunnel ionization, and in particular how an electron reaches the continuum, has raised a great deal of debate. We have applied phase-space tools from quantum optics, such as Wigner quasiprobability distributions and the quantum Liouville equation, to address this problem & look at nonclassicality in enhanced strong-field ionization.
Wigner quasiprobability distributions evolving in time for an initially delocalized wavepacket in a molecule in a static field.
High-order harmonic generation
Matter may respond highly nonlinearly to an intense laser field, generating harmonics of very high order. This process may be viewed as the laser-induced recombination of an electron with its parent ion. Because it happens at well-defined times and in a fraction of the laser cycle, it can be used for ultrafast imaging of matter, attosecond-pulse generation, and one may control HHG using tailored fields. Our work on the topic includes HHG in molecules and inhomogeneous media, control of HHG using bi-chromatic and/or orthogonally polarized fields, and multielectron effects in molecular HHG.

High-order harmonic spectrum computed for N2 beyond the single-active electron, single-active orbital approximation. From CF de Morisson Faria, BB Augstein, Physical Review A 81 (4), 043409 (2010)

Transition probability for a perturbed and unperturbed harmonic oscillator in the presence of a monochromatic laser field, as functions of the field frequency (panel (a)), and of the time (panels (b) and (c)). We consider a cubic non-Hermitian perturbation. From CF de Morisson Faria, A Fring, Journal of Physics A: Mathematical and General 39 (29), 9269 (2006)
Beyond attoscience
My work beyond attoscience focuses on short-pulse propagation and pseudo-Hamiltonian systems.
For short-pulse second harmonic generation, We show that, under the assumption that both the fundamental and harmonic waves are amplitude-modulated, and that the slowly-varying-envelope approximation is valid, general propagation equations can be derived using the Liouville equation.
We were also the first to develop a consistent quantum mechanical formulation for explicit time-dependent pseudo-Hermitian Hamiltonian systems. Further work involves the use of Moyal Brackets in this context.